Operaciones entre Conjuntos
Contenido
Diagrama de Venn
Los es el veenn' son ilustraciones usadas en la teoría de conjuntos cuyo fin es mostrar gráficamente la relación matemática o lógica que hay entre diferentes grupos de cosas (conjuntos).En un Diagrama de Venn, el conjunto universo se representa por un rectángulo, y los conjuntos en su interior se representan por círculos.
Una representación genérica de lo que es un Diagrama de Venn se presenta en la siguiente figura, donde se representa un conjunto universo
 , y dentro de éste un conjunto
, y dentro de éste un conjunto  .
.
Diagrama de Venn
Operaciones entre Conjuntos
Unión de Conjuntos
Sean y
y  dos conjuntos. Se define la unión de
dos conjuntos. Se define la unión de  con
con  , denotada por
, denotada por  (que se lee A unión B), por el conjunto
(que se lee A unión B), por el conjunto
 y
y  , dependiendo de cómo se relacionan entre ellos, se ve como sigue:
, dependiendo de cómo se relacionan entre ellos, se ve como sigue:Ejemplo
Si tenemos los conjuntos y
y  , la unión de ellos es el conjunto
, la unión de ellos es el conjunto
Propiedades de la unión de conjuntos
La unión de conjuntos cumple las siguientes propiedades

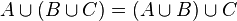

- Si
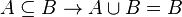
Intersección de Conjuntos
Sean y
y  dos conjuntos. Se define la intersección de
dos conjuntos. Se define la intersección de  y
y  , denotada por
, denotada por  (que se lee A intersección B), por el conjunto
(que se lee A intersección B), por el conjunto
 y
y  , dependiendo de cómo se relacionan entre ellos, se ve como sigue:
, dependiendo de cómo se relacionan entre ellos, se ve como sigue:Ejemplo
Si tenemos los conjuntos y
y 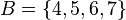 , el conjunto intersección es
, el conjunto intersección es
 y
y  se llaman disjuntos siempre que
se llaman disjuntos siempre que  .
.Propiedades de la intersección de conjuntos
La intersección de conjuntos cumple con las siguientes propiedades
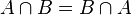


- Si

Diferencia de Conjuntos
Sean y
y  dos conjuntos. Se define la diferencia de
dos conjuntos. Se define la diferencia de  con
con  , denotada por
, denotada por  (que se lee A menos B), por el conjunto
(que se lee A menos B), por el conjunto
 con
con  , dependiendo de cómo se relacionan los conjuntos, se ve como sigue:
, dependiendo de cómo se relacionan los conjuntos, se ve como sigue: con un conjunto
con un conjunto  , en ese orden, es el conjunto formado por todos los elementos que están en
, en ese orden, es el conjunto formado por todos los elementos que están en  pero no están en
pero no están en  .
.Ejemplo
Si tenemos los conjuntos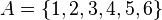 y
y  , entonces el conjunto diferencia de
, entonces el conjunto diferencia de  con
con  es
es
Complemento de un Conjunto
Sea un conjunto dentro de un conjunto universo
un conjunto dentro de un conjunto universo  . Se define el complemento de
. Se define el complemento de  , denotado por
, denotado por 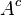 (que se lee A complemento), al conjunto
(que se lee A complemento), al conjunto
Ejemplo
Si tenemos los conjuntos y
y  , entonces el complemento de
, entonces el complemento de  es el conjunto
es el conjunto
Propiedades del complemento de un conjunto
El complemento de un conjunto cumple las siguientes propiedadesPropiedades Combinadas
Se cumplen las siguientes propiedades entre conjuntosEjemplo de operaciones compuestas
Para los conjuntos







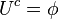





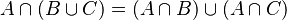








No hay comentarios:
Publicar un comentario