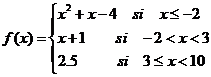En
la historia de las matemáticas se le dan créditos al matemático suizo
Leonhard Euler(1707-1783) por precisar el concepto de función, así como
por realizar un estudio sistemático de todas las funciones
elementales, incluyendo sus derivadas e integrales; sin embargo, el
concepto mismo de función nació con las primeras relaciones observadas
entre dos variables, hecho que seguramente surgió desde los inicios de
la matemática en la humanidad, con civilizaciones como la babilónica, la
egipcia y la china.
Par Ordenados
un
par ordenado es un conjunto de dos elementos A y B que tiene un orden,
al elemento A se lo llama primera componente y al elemento B segunda
componente. se lo representa simbólicamente .(a,b).
(a,b,c)
Producto Cartesiano
sea
2 conjuntos (A y B) no vacíos denominaremos producto cartesiano entre A
y B al conjunto de todos los pares ordenados cuya primera
componente pertenece al conjunto A y la segunda componente al conjunto B
, simbólicamente se lo representa .
AXB
Ejemplo:

Relaciones
una relación establece la correspondencia entre los elementos de un conjunto no vació
A y B .
Generalmente al conjunto A se lo llama conjunto de partida y
al conjunto B conjunto de llegada simbólicamente se lo representa .
R ⊆ AXB

Dominio de una Relación
Dada
una relación construida a partir de los conjuntos A y B los elementos
del conjunto A que establecen correspondencia constituyen el dominio de
la relación.se lo representa Dom R.
Rango de una Relación
Dada
una relación construida a partir de los conjuntos A y B .Loa elementos
del conjunto B que se relacionan con los elementos del dominio de R
.constituye el rango de una relación
.
FUNCIÓN
Una relación de
A y B es una función si y solo si el dominio de la relación es todo el
conjunto de partida y si a cada elemento del dominio le corresponde
un único elemento de rango.

FUNCIONES DE VARIABLE REAL
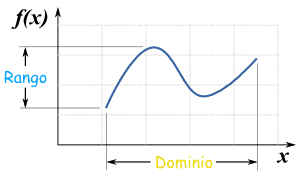
DOMINIO DE LA FUNCIÓN
Sea F una función de variable real ,el conjunto x para el que se encuentra definido constituye el dominio de la función.
Consideraciones
-Cuando sea un cociente que el denominador , si hay X nunca se haga cero .
-cuando tenga una raíz de indice par debo tomar en cuenta de que no sea negativa.
RANGO DE LA FUNCIÓN
Sea F una
función de variable real ,el conjunto de todas las imágenes de los
elementos del dominio constituye el rango de la función.se
representa simbólicamente Rg f.
Pasos
-Despejar X
-El rango sera el conjunto de valores que tome la variable Y.
REPRESENTACIÓN GRÁFICA DE UNA FUNCIÓN
A cada X le pertenece un solo Y .
si F es
una función de A en B entonces la gráfica de F es el conjunto de pares
ordenados de A en B tales que su coordenada son (x,y).
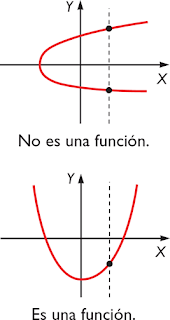
CRITERIO DE LA RECTA VERTICAL
Si cualquier recta vertical intersecta la gráfica en un solo punto es función.
si hay dos puntos al interceptar la recta es relación
TIPOS DE FUNCIONES
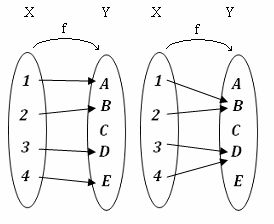
FUNCIÓN INYECTIVA : También es de uno a uno F es inyectiva si cada elemento del rango es imagen exclusiva de un único elemento del dominio ademas la N(A) ≤ N(B).
Ejemplo:


FUNCIÓN SOBREYECTIVA : F es sobreyectiva si Rg:B , ademas N(A)≥ N(B).
Ejemplo:

FUNCIÓN BIYECTIVA : F es una función biyectiva si y solo si es inyectiva y sobreyectiva a la vez.

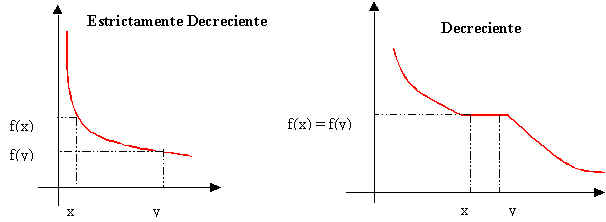
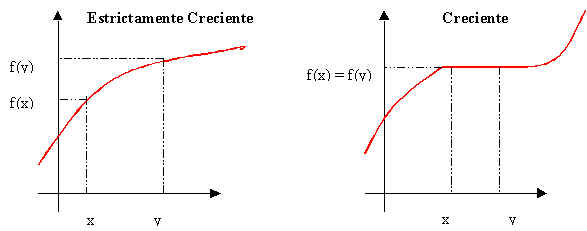
FUNCIÓN CRECIENTE
- Una función y=f(x) es creciente cuando al aumentar la variable independiente, x, aumenta la variable dependiente, y.
- Una función y=f(x) es decreciente cuando al aumentar la variable independiente, x, disminuye la variable dependiente, y.
- Una función y=f(x) es constante cuando al aumentar la variable independiente, x, la variable dependiente, y, no varía.
FUNCIÓN MONÓTONA
Se dice que F
es una función monótona en un intervalo I , si y solo si F es
estrictamente creciente o estrictamente decreciente en ese intervalo.
FUNCIÓN PARES E IMPARES
PAR:Una función f es par si para cada número x en su dominio el número –x también está en su dominio y f(-x) = f(x).
IMPAR: Una función f es impar si para cada número x en su dominio el número –x también está en su dominio y f(-x) = -f(x).
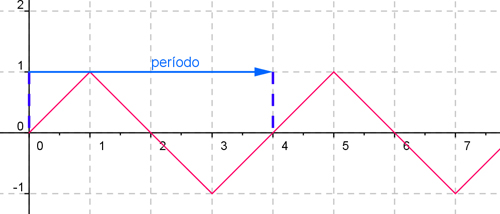
Es aquella función cuyos valores se repiten cada cierto tiempo .dicho tiempo se denomina periodo (T).
FUNCIÓN ACOTADA
Se dice que es
una función acotada , donde M y N son valores reales que se denomina
cota superior y cota inferior , respectivamente.
Cota Superior
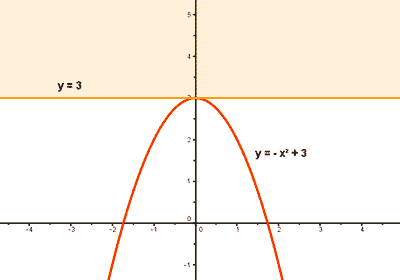
Cota Inferior
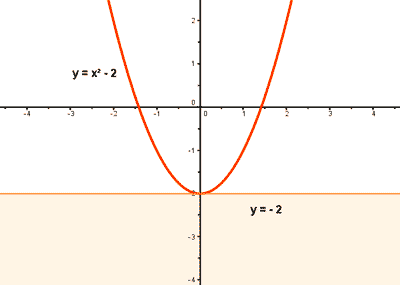
FUNCIÓN DEFINIDA POR TRAMOS
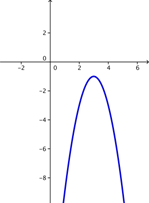
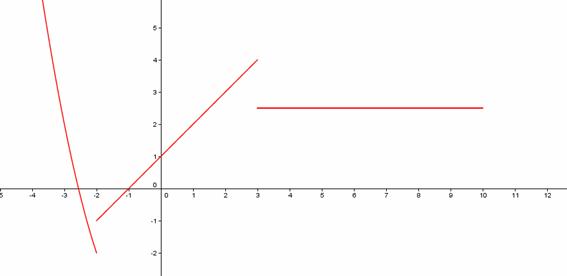
Las funciones definidas a trozos se llaman de esta manera porque tienen una definición diferente en cada tramo en el que están definidas. Por ejemplo,
es una función definida a trozos, en cada “trozo” de su dominio tiene una definición.
Para valores de la variable menores o iguales que −2 la función está definida como x2 + x − 4 ; si la variable está entre −2 y 3 la función es x + 1 y entre 3 y 10 es igual a 2.5.
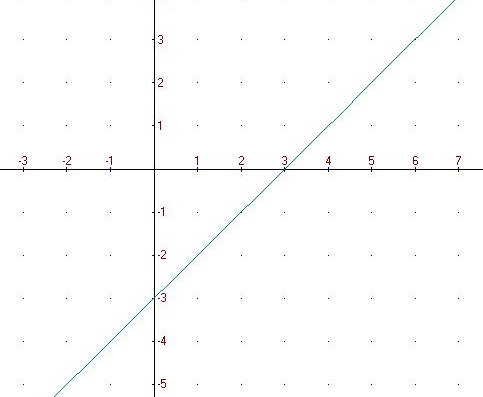
FUNCIÓN LINEAL
Sea A y B Números reales , la función F de R en R cuya regla de correspondencia es f(x)=ax+b.
Ejemplo:

Cortes de X y Y
x=(-b/a,0)
y=(0,b)
a._ (a>0)  (b>0)
(b>0)
 (b>0)
(b>0)
b._ (a>0)  (b<0)
(b<0)
 (b<0)
(b<0)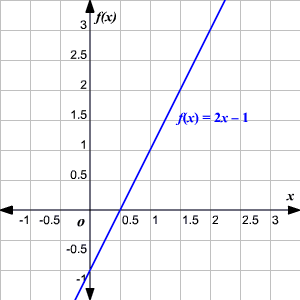
c._ (a<0)  (b>0)
(b>0)
 (b>0)
(b>0)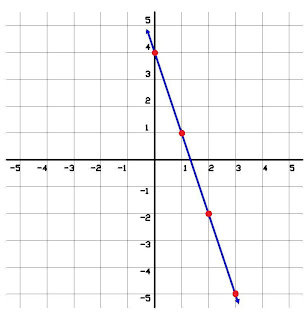
d._ (a<0)  (b<0)
(b<0)
 (b<0)
(b<0)
APLICACIÓN DE FUNCIONES REALES
Ejemplos :
Los costos
fijos de un fabricante son iguales a 10.000 mensuales y el costo de
fabricar una camisa es de 15 dolares si se requiere
representar matemáticamente la función de costos de fabrica.
f(x)=ax+b
f(x)=5x+10.000
(-2.000/5,0)
(0,10.000)
En la ciudad de Guayaquil existían 1420 médicos después de n años el numero de médicos que trabaja en la cuidad viene dado por.
a.cuantos médicos trabajaba en la ciudad al comienzo del año 2014
b.En que año hubo por primera vez mas de 2.000 médicos trabajando en la ciudad.
D(n)=1420+100n
=1420+100(20)
=1420+2000
=3420
D(n)=100(6)+1420
=600+1420
=2020
En el 2000 hubieron mas de 2000 médicos trabajando por primera vez
x=-b/a
x=1420/100
x=-71/5
y=1420
Sea a,b,c números reales con a ≠ 0, la función f de R en R cuya regla de correspondencia es:f(x)=ax2+bx+c
Forma Canónica de la función cuadrática
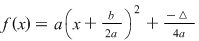
Vértice

- 1 ) Si a > 0 , entonces:
- - La función decrece en el intervalo
- - Crece en el intervalo:
- 2 ) Si a < 0 , entonces:
- - La función crece en el intervalo
- -Decrece en el intervalo:•

Para la Función Cuadrática Existen 6 Tipos de Gráficos
a. (a>0)  (∆>0)
(∆>0)
 (∆>0)
(∆>0)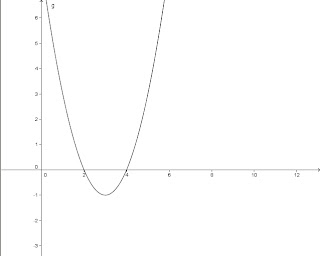
b. (a>0)  (∆=0)
(∆=0)
 (∆=0)
(∆=0)
c. (a>0)  (∆<0)
(∆<0)
 (∆<0)
(∆<0)
d. (a<0)  (∆>0)
(∆>0)
 (∆>0)
(∆>0)
e .(a<0)  (∆=0)
(∆=0)
 (∆=0)
(∆=0)
f. (a<0)  (∆<0)
(∆<0)
 (∆<0)
(∆<0)